Chapter One of The Essential Exponential! For the Future of Our Planet - a book by Albert A. Bartlett
The Essential Exponential! For the Future of Our Planet
by Albert A. Bartlett
University of Colorado at Boulder
with Robert G. Fuller,
Vicki L. Plano Clark
University of Nebraska - Lincoln
and
John A. Rogers,
Westside High School, Omaha NE
Chapter 1: Exponential Recollections, by Albert Bartlett
1) BACKGROUND
Exponential arithmetic first appears in my memory in the beginning calculus course at Colgate University. The applications to the decay of radioactive substances followed in a senior class in modern physics in 1943-44. The exponential aspects of secular equilibrium of the various elements in a radioactive decay chain appeared in K.T. Bainbridge's class in nuclear physics in graduate school at Harvard around 1946. These applications dealt with exponential decay rather than with exponential growth.
My appreciation of exponential growth did not develop until the 1960s after I had been on the physics faculty of the University of Colorado at Boulder for more than a dozen years. The environmental movement was strong in Boulder, and I became much involved in the efforts to protect Boulder from the growth that has now made much of the Colorado Front Range seem so similar to Los Angeles. Boulder's population was growing so rapidly that one could see the cumulative negative effects of population growth on the environment in just a few years. The constant doubling time associated with steady growth of a quantity, and the enormous numbers that resulted from modest numbers of doublings came to impress me more and more. I began to see the utility of being able to say that a quantity N would grow steadily (exponentially) if the rate of change of the quantity, dN/dt was proportional to N. The prime example of this is compound interest on a savings account. In this case N is the number of dollars in the account. Each year N increases by dN/dt because of the addition of interest to the account. And, of course each year the added dN/dt is calculated as a fraction (such as 5%) of N. This meets the condition for steady growth. When I began to apply these numbers to population growth, the predicted sizes became surprisingly and impossibly large in modest periods of time.
2) MY FIRST EXPONENTIAL
My first foray into exponential arithmetic came in the examination, at the simplest level, of the construction of highways in the U.S. If N is the number of miles of highways in the country then, with a couple of assumptions, it is easy to show that dN/dt is proportional to N. As a consequence, the number of miles of highways in the country could be expected to grow exponentially as long as the assumptions remain valid. At a national meeting I had a chance encounter with the editor of the journal, Civil Engineering. When I mentioned this exponential argument to him he expressed interest, so I submitted a short manuscript that was published in the journal's issue of December 1969 under the title, "The Highway Explosion." The use of the word "explosion" was taken from the title of Paul Ehrlich's popular book, "The Population Explosion" which dealt with rapid population growth.
In the 1969-70 academic year I was lecturing in the large introductory physics course that the premed majors were required to take, and in September they asked me if I would be the speaker at the upcoming meeting of their pre-med undergraduate honor society, Alpha Epsilon Delta. I assembled some notes on steady growth, doubling times, and the resulting large numbers, and presented a talk on September 19, 1969. It was well received. Fortunately, I kept my notes for the talk. Little did I know that demand for the talk would continue, that the talk would evolve, and that slightly over 34 years later I would give the talk for the 1500th time.
3) THE POINT OF THE TALK
The talk has evolved over the years, with new materials being added and other materials being removed. The topics included in the talk have broadened, but the focus remains unchanged.
Endless steady growth is the centerpiece of the U.S. and the global economies. It is urgent that we educate people about the arithmetic and consequences of steady growth.
This is summed up nicely in the opening line of the talk:
"The greatest shortcoming of the human race is our inability to understand the exponential function."
4) EARLY HISTORY OF THE TALK
In 1970 the talk was given nine times in Boulder, and once in Denver to the Colorado Legislature
which was having hearings on population. One of the 1970 deliveries was in the TV studio of the University's
Academic Media Services, (AMS). A videotape was made, and copies were made available for sale to the
public. I was offered royalties from the sale of the tapes, but I declined, asking instead that royalties be used to
advance the academic programs of the AMS. New videotape recordings have been made several times since
then, and the number of tapes sold has reached around 2000.
In 1971 the talk was given only four times, and in 1972 there were no invitations to give the talk. This led me to believe that the talk had run its course and had expired. Again, fortunately, I kept my notes. Four invitations came in 1973 and another four in 1974. Six invitations came in 1975. In early 1976 I was invited to present the talk to the Nebraska Section of the American Association of Physics Teachers (AAPT) meeting February 7, at Westside High School in Omaha. This was the first time the talk was presented outside of Colorado and the first time to a section of AAPT. In March of 1976 the talk was given as a physics colloquium at Oklahoma State University with the title "Elementary Physics, The Exponential Function, and the Real World." The talk really took off in 1976, in part because I was elected Vice-President of AAPT. During the four-year service in the presidential chain of AAPT I received many invitations to speak at sections of AAPT all over the country. The talk was delivered 39 times in 1976 including a delivery as "The Arithmetic of Growth" at a national industrial conference at Key Biscayne, Florida.
Originally I talked from notes, but in many of the places where I spoke there was no chalkboard, which deprived me of a major component of classroom communication. So I started making transparencies for the overhead projector. This worked well because the projectors are ubiquitous and making transparencies was quick and easy. At first I made transparencies only of data tables and graphs. Gradually this expanded to the point where essentially all of the important points in the talk were written out on hand-made transparencies for the overhead projector. This use of overhead transparencies seemed to work well with a fast-paced oral delivery, and I began to sense that the talk might be having some impact.
On December 2, 1976 the talk was recorded at the Denver studio of KRMA, Public Television, Channel 6, from which it was broadcast on December 11.
5) "THE EXPONENTIAL FUNCTION"
I began thinking more systematically about exponential arithmetic and about the possibility of writing up a series of articles on various aspects of the exponential function. These would be short articles, each dealing with a single aspect of the exponential arithmetic. The journal The Physics Teacher (TPT) seemed to be an appropriate place to submit such a series so I contacted the editor, Professor Cliff Swartz. Cliff accepted, and the first article by this title appeared in the October 1976 issue of TPT. Thus was born the series of articles "The Exponential Function."
My favorite among the articles is "The Exponential Function XI: The New Flat Earth Society." The late Dr. Julian Simon, economist and business professor, wrote all manner of non-scientific and optimistic predictions about the future. In one publication he wrote that humans had knowledge and resources sufficient to allow us to continue to grow for "seven billion years." I wrote a short manuscript on the interesting and impossible super-astronomically big numbers that would arise from 7 billion years of growth at a modest rate, and I gave it the title "The Exponential Function XI." I submitted it to Cliff Swartz, editor of The Physics Teacher. Some days later, as I was walking to the University, it dawned on me that there was an interesting way to rewrite this paper. If Simon was correct, the Earth had to be essentially infinite in size. This is not easy with a spherical earth. So if Simon is correct, the Earth has to be flat, because a flat earth can be of infinite extent in all three dimensions. I phoned Cliff to ask if I could rewrite the manuscript. He agreed, and so the title of "The Exponential Function, XI" now has the added sub-title "The New Flat Earth Society."
6) BROADENING MY INTERESTS
Then I began to look at the question: how long would the finite reserves of a non-renewable resource last if the annual rate of consumption of the resource was growing steadily. I derived the equation for the life expectancy and proceeded to put in numbers for the reserves of U.S. coal. I was quite accustomed to reading that the U.S. has enormous reserves of coal, "enough for over 500 years at present rates of consumption." I had just purchased my first electronic hand-held calculator, and one of the first calculations I did using the new calculator was to calculate the life expectancy of U.S. coal for some modest growth rate. When I punched the numbers into the calculator, the answer came up "46 years." This was shockingly short, compared to 500 years. I could not believe it. My conclusion was that I must have made an error in entering the numbers. So I entered the numbers again, and the answer again came up as 46 years. I said to myself, "It can't be that short." There must be something wrong with the electronics of my new calculator. So I got pencil, paper, and a table of logarithms and did the calculation by hand. The answer was 46 years! This was an epiphany.
The world is full of people who talk about endless growth in the rates of consumption of resources. This growth shortens the life-expectancy of the resources enormously (for example, from 500 to 46 years). These same people assure the public that there is no need to worry because the resource will last "500 years at present rates of consumption." This is intellectually fraudulent, yet I knew of no one who was or is calling attention to this fraud. I now had a mission.
7) THE TALK: FORGOTTEN FUNDAMENTALS OF THE ENERGY CRISIS
The talk began to focus on the broad impact of growth of populations and of rates of consumption of resources on our daily lives. It also focused on the public misrepresentations of the life expectancies of resources. At this time, the series in TPT was looking at one aspect of the exponential arithmetic at a time. I became impatient with the necessarily slow prospect for covering things in TPT one topic at a time, so I put 6 The Essential Exponential! For the Future of Our Planet together a manuscript, called it "The Forgotten Fundamentals of the Energy Crisis," and submitted it for the program of the Energy Conference at Rolla sponsored by the University of Missouri at Rolla and the Missouri Energy Commission. The paper was accepted and it was presented to the industrial and academic participants at the conference October 12, 1976 in Rolla. The length of the paper was severely restricted so that it could be printed in a fixed number of pages that were allowed each speaker in the volume of the Proceedings of the Conference.
The paper focused on the arithmetic of steady growth, the shortening of the life expectancies of finite resources when rates of consumption were growing steadily, and on the gross misrepresentations of these alarming facts by all manner of academic and industrial "experts." The paper had about as much impact as a pebble thrown in a pool. If there were any ripples, they quickly died out.
The Rolla paper made use of a number of outrageous quotations from prominent academic, political and industrial leaders. This led me to be much more active in scanning the news media for dumb statements about energy being made by prominent people. I was not disappointed. The energy crisis of the mid 1970s was on everyone's mind, and all manner of people were making public diagnoses and recommendations, many of which were simply absurd. I brought many of these quotations into my talk because they would invariably get the attention of people in the audience. On one occasion, a couple of weeks before I was to give my talk at the research laboratory of a major pharmaceutical company, I saw one of the company's ads in a national news magazine. The ad featured a completely unrealistic assertion by a nationally prominent Ph.D. non-scientist who is a prolific author and commentator. I made a transparency of the ad and included it in the talk in such a way as to make obvious the absurdity of the ad's allegations. After the talk, a leader in the lab told me that he would take up the question of the unfounded assertion in the company's ad with the company's top management.
On February 7, 1977 the talk was given as a plenary talk at the national meeting of AAPT in Chicago.
The largest number of times I have given the talk in one day is seven in 1987. At the high school in Brush, Colorado I gave the talk in each of seven class periods in one day.
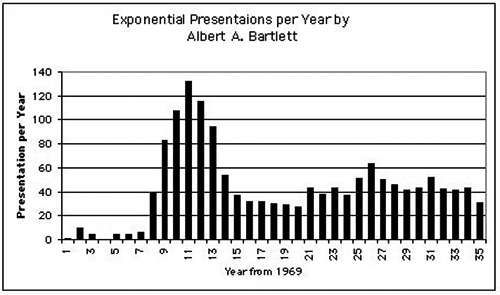
The maximum number of times the talk was given in one year is 132 in 1979.
The talk has been given in 49 of the 50 states (I have no record of ever giving it in New Hampshire), and ten times in Canada. The most distant place where the talk has been given is Riyadh, Saudi Arabia.
I have no idea of the number of times when my actual presentation was videotaped by my hosts.
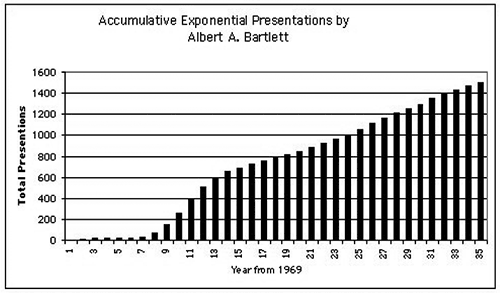
The graph (following this article) shows the number of times the talk has been given as a function of time, starting with the one delivery in 1969.
8) FALLOUT FROM THE TALK
It is always interesting to field questions from the audience after a presentation of the talk. Once a man came to me and identified himself as a banker. He asked if the arithmetic I was discussing was the same as the arithmetic of compound interest. I replied that it was exactly the same. "Oh," he said, "I knew this applied to dollars; I didn't know it applied to people." By every contemporary standard, this man would have been considered to be well educated. He knew what 5% annual interest meant to a savings account, but he had never made the connection to see what a 5% annual growth rate would do to the size of a population.
A second memorable post-talk encounter occurred at Baseline Junior High School in Boulder where I had given the talk slowly to a group of science students. I spread the talk over two one-hour sessions a week apart. After the second talk, two young students came up to me, looked up and asked, "We can understand this. Why can't grown-ups understand it?" That stumped me.
There was another interesting fallout from several years of giving the talk to science students at Baseline Junior High School. Late in the year 2000 I received an e-mail from a lady who identified herself as a student in one of the most prominent business schools in the country. She said that 17 years earlier she had heard my talk at Baseline, and she remembered it. She said that at her business school they talk endlessly about the benefits of growth. Growth seems to be the only criterion for success in the world of business. She asked if I could come out and give my talk on growth to the school. I said I would be happy to do so if she could get the dean to pay my travel expenses. She succeeded, and in January 2001 I spoke to about a hundred students in a class on corporate responsibility. My sense was the students were stunned by the implications of the simple arithmetic. I had a very cordial dinner with students and faculty, and I have not been invited back since. The message about the facts of growth is not well received at business schools.
The talk has been given several times to conventions of petroleum producers and petroleum geologists. After one talk, a petroleum producer got up and announced loudly that if they were to believe what I had said, they were all essentially out of business. He then left the room. Later several people from the audience spoke to me privately to apologize and say that that person had a strong temper.
On one occasion I was invited to give the talk to a large convention of state public utility commissioners. The speaker who followed me was a nationally known Ph.D. non-scientist who argues that we need larger populations, not smaller. He writes books and essays in the New York Times and elsewhere. His opening words to the large audience were, "I disagree with everything Professor Bartlett just said."
On a memorable occasion, I was invited by environmental activists to speak to the city council of a university community. As I faced the nine members of the council, I could see that four of the faces were happy faces, while five faces were angry faces. Later a friend from that community told me that after my talk he had encountered one of those council members (an angry face) and he asked what the member thought of my talk. The council member responded, "It's all smoke and mirrors!"
Not too long ago I gave the talk to a group of retirees, mostly from the University. In the front row
was a retired professor of economics. Throughout the talk I could see that his face showed all manner of
disapproval. In the question period after the talk, he stood up, addressed the audience and in a voice that was
agitated and emphatic he said:
"This is all wrong!"
"This is Malthus all over again! We have proved Malthus was wrong."
After the question period, I talked with him and said,
"You understand the arithmetic. You know that growth can't go on forever."
"Of course," he said, "But we have to grow for now."
"Why for now?" I asked.
"To help poor people!" he replied.
This left me speechless. Once or twice a year news reports tell of new studies that show that the economic gap between the rich and poor is getting larger not smaller, and this is happening throughout a long period of growth of the economy.
9) M. KING HUBBERT
In the course of studying fossil fuel resources, I had come to admire the work of the geophysicist, M. King Hubbert. In a masterful analysis, he noted that the long-term history of the exploitation of a nonrenewable natural resource such as petroleum, the production (barrels per year) has to start at zero, it rises to one or more maxima, and ultimately it returns to zero. A graph of production vs. time then can be approximated by something like a gaussian error curve whose area represents the size of the total resource (barrels) before any of it was used. So if you have some data on the history of recent production and an estimate of the total size of the resource, you can do curve-fitting and arrive at an estimate of the pattern of production in future years. The clarity and simplicity of his analysis is beautiful. He set forth his analysis in a book, "U.S. Energy Resources, A Review as of 1972" which was described as "A Background Paper prepared at the request of Henry M. Jackson, Chairman, Committee on Interior and Insular Affairs, United States Senate pursuant to S. Res. 45, A national Fuels and Energy Policy Study, (Serial No. 93-40 (92-75))." [U.S. Government Printing Office, Washington; 1974]
In 1956 Hubbert used his analysis to predict that U.S. petroleum production would peak between 1966 and 1971. No one took him seriously. Petroleum production in the U.S. peaked in 1970.
I sent him copies of some of my papers, and he very kindly put me on his mailing list for preprints. Hubbert lived near Washington, D.C. In April of 1978 I spoke in Washington, and I was very pleased that he came down to hear me. Afterward, we had a very nice talk over lunch. On several later occasions he phoned me from Washington to tell of ill-considered actions that were pending in Congress and to ask me to contact members of Colorado's congressional delegation to urge them to oppose these actions.
10) THE PAPER: FORGOTTEN FUNDAMENTALS OF THE ENERGY CRISIS
In January of 1978 I became president of AAPT, so the presidential duties and my interest in the exponential arithmetic took up all of my available time and energy. I gave the talk 39 times in 1978. I expanded the Rolla paper and submitted it to Professor John Rigden who was editor of American Journal of Physics. The article was published as "Forgotten Fundamentals of the Energy Crisis" (FFEC) in September 1978.
Requests for reprints streamed in, and physicists teaching at other schools started giving papers at AAPT meetings, describing how they used the materials from FFEC in their classes. With minor modifications, it was reprinted in the Journal of Geological Education, (Vol. 28, No. 1, January 1980, Pgs. 4-35) and in three parts in Mineral & Energy Resources, (Colorado School of Mines, Vol. 22, September 1979, November 1979, and Vol. 23 in January 1980.) In 1993 the paper was included in the Physics Teachers' CD-ROM Toolkit [Physics Info Mall, copyright 1995], a widely used educational resource that was prepared at the University of Nebraska under the direction of Professor Robert Fuller. Environmental groups heard about the paper and asked to reprint it, or parts of it, in their newsletters and journals.
Later, in 1980 John Rigden published a very complimentary editorial, "A Tribute to A.A. Bartlett" in the American Journal of Physics, (Vol.48, May 1980, Pg. 337)
In 1991, Professor Robert Romer, Editor of the American Journal of Physics reported (Am.J.Phys, Vol. 59, March 1991, Pg. 205) that this paper (FFEC) is one of ten "memorable papers" published in the American Journal of Physics, in 1978.
In 1998, Negative Population Growth, a population activist group in Washington, D.C., re-published my "Forgotten Fundamentals..." article on the 20th anniversary of its original publication. I wrote an introduction for this reprinting.
The most recent reprinting of which I am aware was in the Proceedings of the Energy Efficiency and Policy Symposium, November 9, 2000 in Honolulu, Hawaii. I was one of the speakers at the Symposium that was sponsored by the Hawaii State Department of Business, Economic Development and Tourism.
11) ESSAYS IN PHYSICS TEXTS
A number of authors of physics textbooks have invited me to submit topical essays on exponential growth for inclusion in new editions of their texts. These included Raymond Serway, Paul Tipler, and David Halliday and Robert Resnick.
12) SUSTAINED AVAILABILITY
If the ordinate of a graph is the annual rate of consumption of a resource and the abscissa is years, then the area under a section of the graph between two times is the amount of the resource consumed in that interval between the two times. In a conversation, Prof. John Shonle called my attention to the fact that the integral of exp(-kt) from zero to infinity is finite so that a finite quantity of a resource could be put on a declining rate of consumption, and the resource would last forever! I picked up on this and, I put together the paper, "Sustained Availability: A Management Program for Non-Renewable Resources." This was published in the American Journal of Physics, Vol. 54, May 1986, Pgs. 398-402. In this paper I looked at a situation where a nation would extract a resource at the particular declining annual rate that would guarantee that the resource would last forever, but the nation would designate some fraction of the extracted resource for domestic use and the remaining fraction for export. Interesting policy options were explored as the nation changed the fractions of production that were devoted to domestic consumption and to export. Some of the analysis was similar to that for the decay and buildup of isotopes in a chain of radioactive decays. As far as I can tell, this paper has had zero impact, in part because to implement the plan one would have to have a somewhat inflexible schedule of production. This is not compatible with free markets and free trade.
13) APPLICATIONS CLOSE TO HOME
When the results of these simple exponential calculations were applied to the size of the population of Boulder, Colorado, the results were startling. Yet leaders in the City talk endlessly of continuing the population growth of Boulder. It's a "common sense" approach that city leaders say is necessary for what they call "a healthy economy."
At a local conference I participated in a panel on growth. I spoke first, pointing out the large numbers that result from small growth rates in modest periods of time. Then I made the point that it was impossible to have continue for an extended period of time and, most important, that population growth in communities never pays for itself. The next speaker was a prominent Ph.D. non-scientist who said I must be wrong. The only communities she knew of in Colorado that were "healthy" were the ones that were growing. I responded, "Of course, this is because you define 'healthy' as 'growing.'" I reminded her that for us as adults, further growth would be either obesity or cancer, neither of which is healthy.
Administrators of our university talk about the need to stabilize the size of the university enrollment. Yet, with occasional exceptions, each year's entering freshman class is larger that that of the preceding year. Apply an annual growth rate of a mere 2% to a total university enrollment of 26,000 and in 100 years you have an enrollment of around 200,000! I have taken pains to prepare extrapolations of current growth rates in the University using spreadsheet tables and graphs that I have circulated to administrators. Nothing happens. The administrators are in a bind. Colorado's population is growing by over 2% per year. If the University does not grow in enrollment at something like the growth rate of Colorado's population, then the University may risk losing its "flagship" status in higher education in Colorado. This results in inexorable growth in the size of the freshman class that is admitted each year and in the total enrollment of the campus.
14) WASHINGTON, D.C.
For several years I served on the Board of Directors of the Carrying Capacity Network (CCN), a public education and lobbying group in Washington, D.C. that focuses on the problems of the growing population in the U.S. Here I met academics from the biological and social sciences who knew their way around the power corridors of Washington. The Network sponsored conferences at which I was invited to speak, and on several occasions the CCN people arranged for me to give my talk to staff members from the House and Senate. Occasionally members of Congress heard the talk. Hon. Vernon Ehlers (R-Michigan) got up after one talk, turned and addressed the audience (members of congressional staffs) and told them that he knew me and knew that what I was saying was correct and that it was important that they pay attention. Hon. Roscoe Bartlett (R-Maryland) was impressed, and twice later he invited me to testify before subcommittees of the House that are dealing with energy. (To the best of our knowledge, Rep. Bartlett and I are not related)
This service in Washington brought me into contact with people outside of science who were concerned about the problems of population growth. Exponential arithmetic is not normally a part of their background. In particular, I came to know Prof. Virginia Abernethy. She is an anthropologist who was a member of the faculty at the Medical School of Vanderbilt University. She was also editor of the journal Population & Environment. During a break in a meeting, I asked her if it might help if I prepared a tutorial on the elements of exponential arithmetic as it is applied to problems of population and then submitted it for consideration for publication in her journal. She responded favorably, and in the years that followed, the tutorial and several other manuscripts were published in Population & Environment.
15) SUSTAINABILITY
In the late 1980s we began to hear the term "sustainability" used in all manner of discussions of growth and development.
"Sustainability" has to mean "for a long time," where "long" means compared to a human lifetime. The basic exponential arithmetic shows that growth of numbers of real things can't continue for long times. This simple observation leads to the First Law of Sustainability. "Growth of populations and / or growth in rates of consumption of resources, cannot be sustained." It follows that the term "sustainable growth" is an oxymoron. It remains a mystery as to why all the ardent advocates of sustainability talk about everything except the First Law of Sustainability.
I put together the simple facts about sustainability into the paper "Reflections on Sustainability, Population Growth and the Environment," which was published in Population & Environment. (Vol.16, No.1, Sept. 1994, Pgs. 5-35) Included in the paper is a compilation of the Laws of Sustainability that seemed to me to follow from the obvious arithmetic and other facts. In 1997 I received a request from Robert D. Day, Executive Director of the Renewable Resources Foundation of Bethesda, Maryland to reprint the "Reflections..." article in the Renewable Resources Journal. (Vol.15, No.4, Winter 1997-98, Pgs. 6-23) The article was republished with a few minor changes from the 1994 version.
Tragically, "sustainability" remains a buzz-word that is invoked by environmentalists and others to describe their various enterprises, whether or not these enterprises are sustainable.
16) POPULATION
Although it took me decades to recognize it, the growth of populations is clearly the most serious problem faced by the human race. It all seems so obvious now. The world population is increasing by about 75-80 million people every year, while the U.S. population is growing by over 3 million per year. The numbers would suggest that the U.S. problem is small compared with the world problem, but there is more to it. If you factor in the estimate that a child born in the U.S. will, in that child's lifetime, have something like 10 to 50 times the impact on world resources as will a child born in an undeveloped country then you reach the conclusion that the world's most serious population growth problem is right here in the U.S.
When speaking of overpopulation, it is politically correct to refer to "those people," meaning people in distant undeveloped nations. It is politically incorrect to speak of the United States being overpopulated.
The ultimate irony is that each year wildlife experts tell us how the herd of elk in Rocky Mountain National Park has exceeded the carrying capacity of the Park and how steps must be taken to reduce the size of the herd. At the same time the population of the U.S. has exceeded our carrying capacity (we import an appreciable fraction of our food) and yet, with all of our academic and technical expertise, there seems to be no recognition of the increasing perils of human overpopulation.
17) ACKNOWLEDGMENTS
Ever since I joined the faculty in 1950, my colleagues in the Department of Physics of the University of Colorado at Boulder have been completely supportive of my work. I want to thank them for their continuing help and interest. In particular, Professors Jack Kraushaar and Robert Ristinen have helped me a great deal as they were preparing their successful texts on the problems of energy and society.
The late Elwood Miller and Kate Albers of the University's Information Technology Services have been instrumental in the preparation of the several editions of the videotapes of my talk. I thank them most sincerely for all of their help.
I wish to express my deep and sincere thanks to all of the physicists, particularly in the American Association of Physics Teachers, and to the others who have given me support, encouragement, and constructive suggestions throughout the years that the forgotten fundamentals of the energy crisis has been my central professional endeavor. The contributions of literally hundreds of people have been enormously helpful in improving my understanding of the exponential concepts and of their utility and applicability in everyday life. I want especially to thank Professor Cliff Swartz who, as editor of The Physics Teacher, started the ball rolling with his publication of many of the early pieces, "The Exponential Function," Professor John Rigden who, as editor of the American Journal of Physics published the full initial version of the "Forgotten Fundamentals of the Energy Crisis," and Professor Virginia Abernethy, the editor of Population & Environment for her advice and support in publishing several of my manuscripts.
Dr. M. King Hubbert was instrumental in expanding my understanding of the patterns of the rates of consumption of finite resources. His work in this area was monumental without being mathematically complicated or difficult. I treasure his friendship.
It was in Washington that I met Professor Garrett Hardin whose essay "The Tragedy of the Commons" remains one of the most cogent expositions of the causes of human actions that are destructive of the environment. His insights and the scholarly precision of his writing remain models for us all. He understood the population problem and he gave me both concrete help and enduring inspiration.
I believe I met Dr. John Tanton at the same conference where I met Garrett Hardin. John is remarkable for his energy and insight into the problems of population. He is closely associated with the journal, The Social Contract which published a special edition (Vol.8, Spring 1998) to commemorate the 200th anniversary of the famous and controversial essay on population by Robert Malthus. Malthus was a mathematician, and he understood the problems associated with growth of populations. I was honored to be invited to submit a contribution to this commemorative issue of The Social Contract. ("Malthus Marginalized: The Massive Movement to Marginalize the Man's Message")
For several years I gave my talk at an environmental law conference that is held each March at the Law School of the University of Oregon. It was at one of these conferences that I met Dr. Walter Youngquist, a global resource geologist. We quickly came to recognize that we shared many of the same concerns and since then we have corresponded regularly. His book "Geodestinies" is a tour-de-force presentation of the resource base of the materials needed in our society, as well as a history of the rate of "production" of these resources. His knowledge of fossil fuels is encyclopedic, and he has kindly shared with me all manner information and suggestions.
It is particularly appropriate to thank Professor Robert G. Fuller, Vicki L. Plano Clark, and John A. Rogers who have done the work of assembling these scattered publications and arranging for them to be published in a single document. Their interest and work are greatly appreciated.
I reserve my greatest thanks for my wife and family who have been enormously supportive of my exponential educational efforts over the years.
So, welcome to the world that has been characterized as "smoke and mirrors."